2019数学建模校内赛实录

Dongchuan Road Station, Minhang, Shanghai
为期七天的建模比赛终于结束了,这也是我第一次参加建模比赛,比赛当中我们倾注了不少的心血与热情,而且也收获良多,下面就来简要谈谈这次比赛的过程与感想吧。
建模之前
大概在五月末的时候我看到了比赛通知,因为这是全校学生都可报名的校内热身赛,而且比赛时间被放在了暑假,比赛时长也放宽至了七天,对我这种建模新手相对比较友好,因此就有了强烈的报名意向。
在我准备寻找队友的时候,Y大佬找到我,问我是否愿意参加这个比赛。由于比赛期间及其之后我都没有要紧的安排,因此我没有做过多的犹豫就答应了。
因为比赛时长放宽至了七天,比一般的建模比赛多出不少,因此前两天我们都没有特别关注这个比赛,只是把题目稍许浏览了一遍,第二天晚上才慢慢开始启动。
选题
本次比赛提供了三道题,其中A题主要任务是通过时间序列分析预报期货走势,B题主要任务是建立数学模型对学科竞赛的评委水平进行评价,C题主要任务是建立模型进行潮汐的分离与绘制同潮图。
在经过了讨论之后,我们决定对C题进行求解。虽然C题的题面较为生涩,但是在阅读了C题后面所附的参考文献( 风暴潮数值同化研究和高度计资料拟合方法研究 )以后,我们对问题有了大致理解与思路。相比之下A题的方法与任务过于明确,很有可能导致最后变成纯粹的算法竞赛,而B题要求完成的任务则太多并且问题较为开放,可能会影响全局的时间分配。
C题的题干很长,下面仅做部分节选:
潮汐潮流运动是海洋中的基本运动之一,它是动力海洋学研究的重要组成部分。在大陆架浅海海洋中,对潮汐潮流的研究更具重要性。
从区域海洋潮汐的数值模拟的现状来讲,四个主要分潮的单一分潮的数值模拟与同化可以得到令人满意的结果,但其它分潮的单一分潮的数值模拟与同化结果却难以使人满意。长周期分潮的获取,目前已基于全球长周期分潮数值模拟手段的报道,但其面临的困境,与其它较弱分潮面临的困境没有差别。
从各分潮的调和常数获取的发展史来说,通过对已有观测结果进行插值曾经是首选,但发展过程中逐渐被数值模拟方法所取代。高度计资料的出现,引发部分学者开展了插值方法的研究,并取得了一些值得一提的结果,尽管被所谓的主流方式淹没,但也难掩其光芒所在。鉴于目前已有高度计资料作为支持,其它分潮及长周期分潮的调和常数获取的插值方法研究大有可为。
根据以上的介绍以及所提供的的数据,请完成如下任务:
1.根据星下观测点各主要分潮($M_{2},S_{2},K_{1},O_{1}$)的潮汐调和常数,沿轨道作图后,可发现潮汐调和常数在沿轨道方向,在空间有细结构,而此细结构是内潮对正压潮的调制;请设法对沿轨道的各分潮的潮汐调和常数进行正压潮和内潮的分离。
2.利用数据插值或拟合方法给出南海的各主要分潮($M_{2},S_{2},K_{1},O_{1}$)的同潮图,并利用潮汐验潮点的调和常数给予评价或验证;特别需要指出的是,需明确所利用方法的优势。
题目提供如下数据:
1.地形数据,来自ETOPO5,分辨率为$5’ \times 5’$ ,此处数据度范围$2^{\circ} \backsim 25^{\circ} N,99^{\circ} \backsim 122^{\circ} E$
2.中国近海及周边海域217个验潮站的资料,包括4个分潮($M_{2},S_{2},K_{1},O_{1}$)的潮汐调和常数
3.南海沿轨星下观测点的4个分潮($M_{2},S_{2},K_{1},O_{1}$)的潮汐调和常数
建模
由于这个题目具有非常强的专业性,并且涉及到的专业知识(潮汐学)我之前从未有过接触,因此不免要通过各种渠道(中国知网、图书馆等)来查阅文献以启发思路。
某大佬:“建模大赛就是自学大赛。”
好在搜集到的论文以及提供的参考文献提供了丰富且有建设性的资料,我们最后基本上建立了能够解决问题的模型。
第一问的主要思路就是高次多项式拟合,也就是说,可以将正压潮与内潮的常数表示为如下形式:
其中,$y$代表点的纬度值。
模型中进行高次多项式拟合的方法与常规方法有所不同,参考文献中对其大致介绍如下:
Dushaw(2002)在夏威夷海区采用300km滑动平均的方法进行滤波,并证实对$HcosG$与$HsinG$进行滤波的结果要好于对$H$与$G$进行滤波的结果($H$与$G$分别为海表面振幅与迟角)
第二问的任务是通过插值或者拟合方法绘制出南海各主要分潮的同潮图,一个效果较好的拟合方案如下:
对于在轨道上的点,可以直接通过多项式拟合的方法求解其调和常数,如果该点不在轨道上,则根据该点到其最近的两条上(下)行轨间的距离比,在这两条上(下)行轨间的下(上)行轨上可以找到与该点具有相同距离比的一系列点,对这些点的调和常数进行多项式拟合,根据拟合得到的多项式从而求得该点的调和常数。
遗憾的是,由于能力与时间的限制,我们最后没有通过这种方法绘制同潮图,而是选用了基于Delaunay三角剖分的自然插值法,虽然也取得了不错的效果,但是并没有完全达到我们的预期。
至于建模过程中代码的编写,可以用放飞自我来形容。因为对Matlab以及Python提供的各种工具并不是很熟悉,以至于很多代码都是一边翻文档一边写的。编码风格也基本可以说是惨不忍睹,许多代码要解决的问题基本相同,仅仅是数据不同,而我采取的措施是—复制代码然后直接在代码中修改数据或者修改数据文件的路径。
以下是建模过程中制作的一些图表:
绘制的星下轨迹图
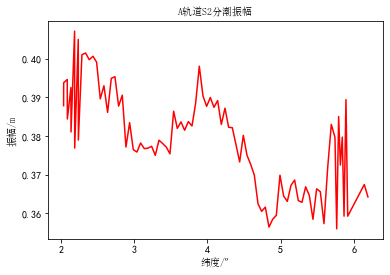
沿轨道绘制的分潮振幅
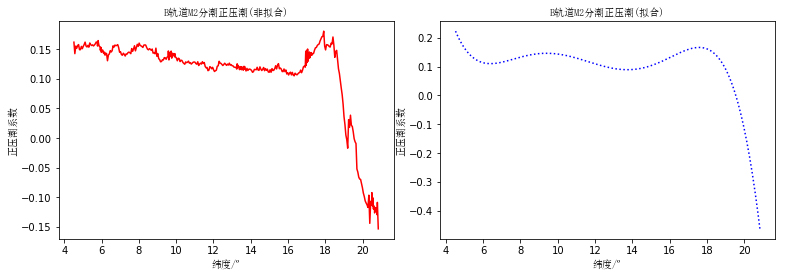
通过多项式拟合分离正压潮
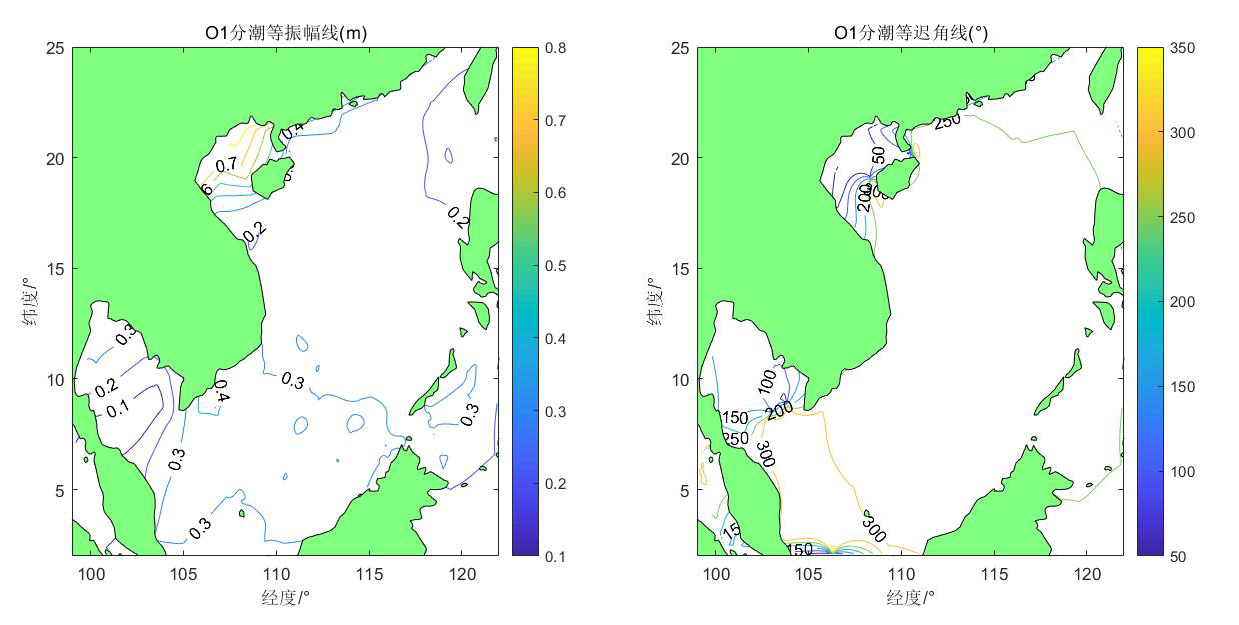
绘制的同潮图
感想
在大家的努力下,比赛最后我们按时地提交了论文,比赛的过程虽然辛苦但是也很有意思,与队友的合作也非常愉快。这次比赛也使我感想良多:
- 数理基础还是有待加强,因为能力以及时间的原因,我们并未使用上文提到的效果较好的拟合方法绘制同潮图,这也是比较遗憾的地方
- 要熟练掌握各种编程工具,这样可以节省很多编写代码的时间,从而可以将更多精力聚焦在模型建立以及优化上
- 对数学建模的一些基本流程以及一些常用模型要加深理解并熟练运用
当然,以上所提及的素质以及能力的提升是一个系统性的工程,并不是一蹴而就的。