抽象代数习题--格与布尔代数部分

如有疏漏，敬请指正

1

题目:
Draw the lattice diagram for the power set of $X = \lbrace a, b, c, d \rbrace$ with the set inclusion relation $\subseteq$.
解答:
示意图如下所示: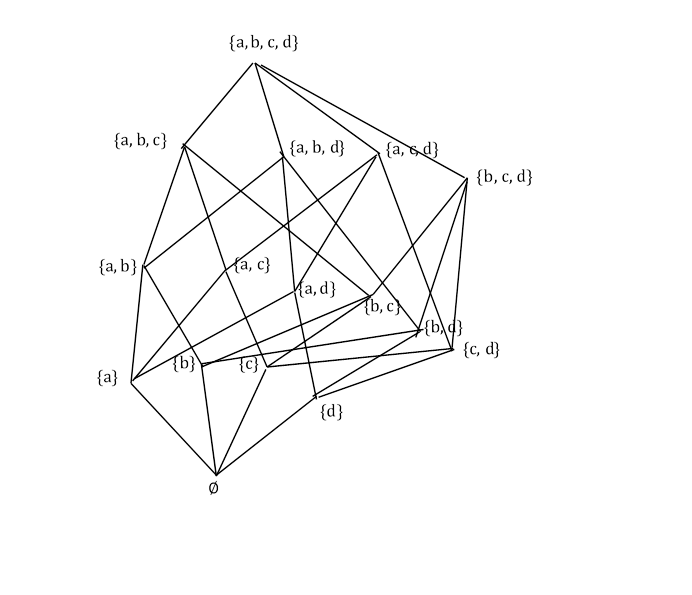

2

题目:
Let $B$ be the set of positive integers that are divisors of 30. $a \preceq b$ on $B$ is defined by $a \mid b$. Prove that $B$ is a Boolean algebra. Find a set $X$ such that $B$ is isomorphic to $\mathcal{P} (X)$
解答:
(1)
易知，$B=\lbrace 1,2,3,5,6,10,15,30 \rbrace$
其中的最大元素$I=30$，最小元素$O=1$
定义$\vee$运算为$\mathbb{Z}$上的乘法运算，$\land$运算为$a \land b=gcd(a,b)$
则对任意$a \in B$，有$a \vee a’ = I$且$a \land a’=O$
由最大公约数的性质可知

$$a \cdot gcd(b,c)=gcd(ab,ac)$$

即$a \vee (b \land c)=(a \vee b) \land (a \vee c)$
因此$B$有补且满足分配律
综上，$B$是一个布尔代数
(2)
令$X=atom(B)=\lbrace 2,3,5 \rbrace$
由同构定理可知

$$B \cong \mathcal{P} (X)$$

3

题目:
Show whether $\mathbb{Z}^{+}$ with $a \preceq b$ defined by $a \mid b$ is a lattice, and whether it is a Boolean algebra.
解答:
(1)
易知，关系$\mid$是一个偏序关系
且$\mathbb{Z}^{+}$是一个格
对任意$a,b \in \mathbb{Z}^{+}$，其上确界为$lcm(a,b)$，下确界为$gcd(a,b)$
(2)
$\mathbb{Z}^{+}$不是布尔代数
因为找不到最大值$I$，使得对任意$a \in \mathbb{Z}^{+}$，有$a \preceq I$

4

题目:
Let $G$ be an Abelian group and $X$ be the set of subgroups of $G$ ordered by $\subseteq$. Prove that the least upper bound of two subgroups $H$ and $K$ in Boolean algebra $X$ is $HK$.
解答:
对任意$h_{1},h_{2},h \in H,k_{1},k_{2},k \in K$，有

$$h_{1}h_{2},k_{1}k_{2} \in HK$$ $$hk=kh \in HK$$ $$k^{-1} h^{-1} = h^{-1} k^{-1} \in HK$$

因此$HK$也是一个阿贝尔群
易知$H,K \subset HK$，因此$HK$是$H$与$K$的上界
假设$H,K \subseteq P \subset HK$
令$i \in H,j \in K,i \neq j$且$ij \notin P$
由题意得$P$也是群，且$i,j \in P$
那么必有$ij \in P$
矛盾！
因此$H$与$K$的上确界是$HK$

5

题目:
The order of any finite Boolean algebra must be $2^{n}$ for some positive integer $n$.
解答:
令$A$是有限布尔代数$B$中所有原子组成的集合，且$\mid A \mid = n$
那么由幂集的性质可得$\mid \mathcal{P} (A) \mid = 2^{n}$
由同构定理可得

$$B \cong \mathcal{P} (A)$$

因此$\mid B \mid = 2^{n}$
即任意有限布尔代数的阶都是$2^{n}$，其中$n$是正数

6

题目:
Let $B$ be a Boolean algebra. Prove that

• $a=b$ iif $(a \land b’) \vee (a’ \land b)=O$ for $a,b \in B$
• $a=O$ iif $\forall b \in B, (a \land b’) \vee (a’ \land b)=b$

解答:
(1)
当$a=b$时，有

$$(a \land b') \vee (a' \land b)=(a \land a') \vee (a' \land a) = O \vee O=O$$

当$(a \land b’) \vee (a’ \land b)=O$时，易知

$$a \land b'=O \; \mathrm{and} \; a' \land b=O$$

那么有

$$a \preceq b \; \mathrm{and} \; b \preceq a$$

因此由偏序关系的反对称性

$$a=b$$

(2)
当$a=O$时，有

$$(a \land b') \vee (a' \land b)=O \vee b=b$$

当$(a \land b’) \vee (a’ \land b)=b$时
因为该式对所有$b \in B$都适用，那么假设$b=O$
此时有

$$(a \land I) \vee (a' \land O)=O$$ $$a \vee O=O$$ $$a=O$$

综上，$a=O$当且仅当对任意$b \in B$，有$(a \land b’) \vee (a’ \land b)=b$