数值分析学习笔记--数值积分与数值微分

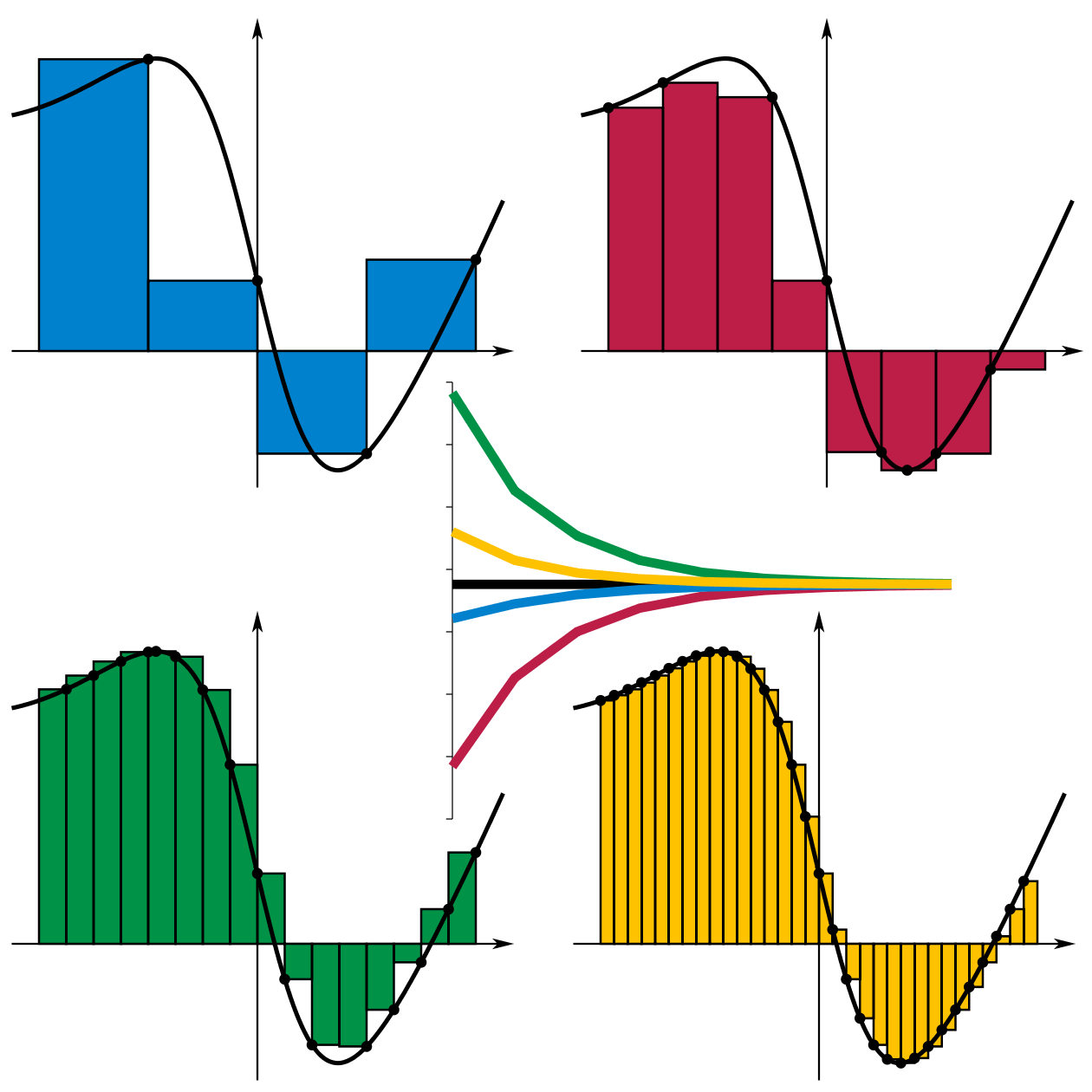
确定的子区间上不同的取样方式构成的Riemann和

如有疏漏，敬请指正

绪论

在微积分学中，我们可以使用牛顿-莱布尼茨公式计算定积分

$$\int_{a}^{b} f(x)dx=F(b)-F(a)$$

但是，当被积函数以点列形式给出，或者被积函数的原函数无法用初等函数表示时(如$\int_{1}^{2} sinx^2 dx$)，则不能使用牛顿-莱布尼茨公式计算。

已知定积分是Riemann和的极限，即

$$\int_{a}^{b} f(x) dx=\lim_{\Delta x_i \to 0}\left(\sum_{i=0}^{n-1}f(x_i)\Delta x_i \right)$$

在数值积分中，用有限项的和近似这一极限，通常由函数在离散点列函数值的线性组合形式给出。记

$$I(f)=\int_{a}^{b}f(x)dx,I_{n}(f)=\sum_{i=0}^{n} \alpha_{i} f(x_{i})$$

代数精度是衡量数值积分公式的重要标准。

记$[a,b]$上以$\lbrace x_i,i=0,1, \cdots ,n \rbrace$为积分节点的数值积分公式为

$$I_n(f)=\sum_{i=0}^{n} \alpha_i f(x_i)$$

若$I_n(f)$满足

$$E_n(x^k)=I(x^k)-I_n(x^k)=0,k=0,1, \cdots ,m$$

而

$$E_n(x^{m+1}) \neq 0$$

则称$I_n(f)$具有$m$阶代数精度。

当$I_n(f)$具有$m$阶代数精度时，对任意的不高于$m$次多项式$f(x)$都有$I(f)=I_n(f)$。

插值型数值积分

对给定的被积函数$f(x)$在$[a,b]$上的点列$\lbrace (x_i,f(x_i )),i=0,1, \cdots ,n \rbrace$，作Lagrange插值多项式$L_n(x)$进行近似，即

$$\int_{a}^b f(x)dx \approx \int_{a}^b L_n(x)dx = \int_{a}^b \sum_{i=0}^{n} l_i(x)f(x_i) dx=\sum_{i=0}^n \left[ \int_{a}^b l_i(x)dx \right]f(x_i)$$

记$\alpha_i = \int_{a}^{b} l_i(x)dx$，则

$$I_n(f)=\int_a^b L_n(x) dx = \sum_{i=0}^n \alpha_i f(x_i)$$

数值积分误差为

$$E_n(f)=\int_{a}^b R_n(x)dx=\frac{1}{(n+1)!} \int_{a}^{b} f^{(n+1)}(\xi(x)) \prod_{i=0}^n(x-x_i)dx$$

或者

$$E_n(f)=\int_{a}^{b} f[x_{0},x_1,\cdots, x_n,x] \prod_{i=0}^n(x-x_i)dx$$

若$f(x)$是一个不高于$n$次的多项式，由于$f^{(n+1)}(x)=0$，而有$E_n(f)=0$。因此$n$阶插值多项式形式的数值积分公式至少有$n$阶代数精度。

牛顿-柯特斯积分

对积分区间$[a,b]$进行$n$等分，记步长为$h=\frac{b-a}{n}$，取等分点$\lbrace x_{i}=a+ih,i=0,1, \cdots ,n \rbrace$为数值积分节点，构造Lagrange插值多项式$L_n(x)$

$$\int_{a}^b f(x)dx \approx \int_a^b L_n(x) dx$$

是为Newton-Cotes积分。

梯形积分

记

$$T(f)=\frac{b-a}{2}[f(a)+f(b)]$$

为梯形积分公式。

其几何意义是用梯形面积近似代替积分值。

梯形公式具有一阶代数精度。

梯形公式的截断误差为

$$E_1(x)=\frac{f''(\eta)}{2!}\int_{a}^{b}(x-a)(x-b)dx=-\frac{f''(\eta)}{12}(b-a)^3$$

其中$a \leq \eta \leq b$。

Simpson积分

记

$$S(f)=\frac{b-a}{6}\left[ f(a)+4f \left( \frac{a+b}{2} \right)+f(b) \right]$$

为Simpson积分公式。

其几何意义是用过3点的抛物线面积近似代替积分的曲边面积。

Simpson公式具有三阶代数精度。

Simpson积分公式的误差为

$$E_2(f)=-\frac{f^{(4)}(\eta)}{2880} (b-a)^5,a \leq \eta \leq b$$

Newton-Cotes积分系数

构造插值函数$L_n(x)$，得

$$\int_{a}^{b}L_n(x)dx=\sum_{i=0}^{n} \alpha_i f(x_i)$$

记

$$\alpha_i=(b-a)c_i^{(n)}$$ $$c_i^{(n)}=\frac{(-1)^{n-i}}{i!(n-i)!n} \int_{0}^{n} t(t-1) \cdots (t-i+1)(t-i-1) \cdots (t-n) dt$$

为Newton-Cotes系数。在取等距节点时，$c_i^{(n)}$与积分节点和积分区间无直接关系，只与插值的节点总数有关。

Newton-Cotes积分系数$\lbrace c_k^{(n)},k=0,1, \cdots ,n \rbrace$，当$n \leq 7$时数值积分公式$I_n(f)=(b-a) \sum_{k=0}^{n} c_k^{(n)}f(x_k)$是稳定的。

复化数值积分

复化梯形积分

复化梯形积分是计算数值积分的最朴素方法。

对$[a,b]$作等距分割，$h=\frac{b-a}{n}$，$\lbrace x_i=a+ih,i=0,1, \cdots ,n \rbrace$，记$n$等分的复化梯形公式为$T_n(f)$，则

$$T_n(f)=h \left[ \frac{1}{2} f(a)+ \sum_{i=1}^{n-1} f(a+ih)+\frac{1}{2}f(b) \right]$$

复化梯形公式的截断误差为

$$E_n(f)=-\frac{(b-a)^3}{12n^2}f''(\xi) ,a \leq \xi \leq b$$

可以看出截断误差按照$\frac{1}{n^2}$的下降速度下降，可以证明，只要$f(x)$在$(a,b)$上有界并黎曼可积，当分点无限增多时，复化梯形公式收敛到积分$I(f)=\int_a^b f(x) dx$。

记$M_2=\max_{a \leq x \leq b} \mid f’’(x) \mid$，则

$$\mid E_n(f) \mid \leq \frac{(b-a)^3}{12n^2}M_2 = O\left( \frac{1}{n^2} \right)$$

对于任意的误差控制小量$\epsilon >0$，若

$$\frac{(b-a)^3}{12n^2}M_2< \epsilon \; \mathrm{or} \; n \geq \left[ \sqrt{\frac{(b-a)^3M_2}{12\epsilon}} \right]+1$$

则有$\mid E_n(f) \mid < \epsilon$，$[\cdot ]$表示取其最大整数。

复化Simpson积分

把积分区间$2m$等分，记$n=2m$，其中$n+1$为节点总数，$m$为积分子区间总数。记$h=\frac{b-a}{n},\lbrace x_i=a+ih,i=0,1, \cdots ,n \rbrace$，在每个子区间$[x_{2i},x_{2i+2}]$上使用Simpson积分公式，得到复化Simpson公式$S_n(f)$为

$$S_n(f)=\frac{h}{3} \left[ f(a)+4\sum_{i=0}^{m-1} f(x_{2i+1})+2\sum_{i=1}^{m-1} f(x_{2i})+f(b) \right]$$

复化Simpson积分的截断误差是

$$I(f)-S_n(f)=\frac{-(b-a)^5}{180n^4}f^{(4)}(\xi),a \leq \xi \leq b$$

可见截断误差按照$\frac{1}{n^4}$的下降速度下降。可以证明，只要$f(x)$在$(a,b)$上有界并黎曼可积，当分点无限增多时，复化Simpson公式收敛到积分$I(f)=\int_a^b f(x) dx$。

记$M_4=\max_{a \leq x \leq b} \mid f^{4}(x) \mid$，则

$$\mid E_n(f) \mid \leq \frac{(b-a)^5}{2880m^4}M_4 = O\left( \frac{1}{m^4} \right)$$

对于任意的误差控制小量$\epsilon >0$，若

$$\frac{(b-a)^5}{2880m^4}M_4< \epsilon \; \mathrm{or} \; m \geq \left[ \sqrt[4]{\frac{(b-a)^5 M_4}{2880\epsilon}} \right]+1$$

则有$\mid E_n(f) \mid < \epsilon$。

自动误差控制

对于给定误差$\epsilon$，通过估计函数的导函数的界的方法能计算出$n$，然而这种方法较为繁琐。因此在实务中往往使用事后估计确定误差。

对$[a,b]$上n等分，$h_n=\frac{b-a}{n}$，则

$$T_n(f)=h_n \left[ \frac{1}{2} f(a)+\sum_{i=1}^{n-1}f(x_n)+\frac{1}{2} f(b) \right]$$

那么

$$T_{2n}(f)=\frac{1}{2} [T_n(f)+H_n(f)]$$

其中

$$H_n(f)=h_n \sum_{i=0}^{n-1} f(x_{i+\frac{1}{2}})$$

或者表示为

$$T_{2n}(f)=\frac{1}{2} T_n(f)+h_{2n} \sum_{i=1}^{n}f(a+(2i-1)h_{2n})$$

其中

$$h_{2n}=\frac{b-a}{2n}$$

类似的，可以获得积分节点为$n$和$2n$的Simpson求积公式的关系式

$$S_{2n}(f)=\frac{1}{2} S_n(f)+\frac{1}{6}(4H_{2n}(f)-H_{n}(f))$$

对于任意的误差控制量$\epsilon >0$，要$\mid I_n(f)-T_{2n}(f) \mid < \epsilon$，只需$\mid T_{2n}(f)-T_{n}(f) \mid < 3 \epsilon$即可，这种方法更加简单直接。

Romberg积分

Romberg算法从梯形积分逐步外推，在不增加计算量的前提下提高了误差精度。

将$T_{n},S_{n},C_{n}, \cdots$分别用$R_{k,j}$表示，则Romberg计算公式为

$$R_{k,j}=R_{k,j-1}+\frac{R_{k,j-1}-R_{k-1,j-1}}{4^{j-1}-1},k=2,3, \cdots$$

持续迭代过程，直到$\mid R_{k,k}-R_{k-1,k-1} \mid$小于给定控制精度。

其中

$$R_{1,1}=h\frac{f(a)+f(b)}{2}$$ $$R_{k,1}=\frac{R_{k-1,1}+h_{k-1}\sum_{i=1}^{2^{k-2}}f(a+(2i-1)h_k)}{2}$$ $$h_k=\frac{h}{2^{k-1}}$$ $$h=b-a$$

重积分计算

以矩形域上的二重积分为例，讨论二重数值积分

二重积分的复化梯形公式

对区间$[a,b]$和$[c,d]$分别选取正整数$m$和$n$，在$x$轴和$y$轴上分别有步长

$$h=\frac{b-a}{m},k=\frac{d-c}{n}$$

则

$$\int_{a}^{b} \int_{c}^{d}f(x,y)dxdy=hk\sum_{i=0}^{m} \sum_{j=0}^{n} c_{i,j}f(x_i,y_j)$$

积分区域的4个角点的系数是$\frac{1}{4}$，4个边界的系数是$\frac{1}{2}$，内部节点的系数是1。
截断误差为

$$E(f)=-\frac{(d-c)(b-a)}{12} \left( h^2 \frac{\partial^2f(\eta,\mu)}{\partial x^2}+k^2 \frac{\partial^2 f(\bar{\eta},\bar{\mu})}{\partial y^2} \right)$$

其中$\eta, \bar{\eta} \in [a,b],\mu,\bar{\mu} \in [c,d]$

二重积分的复化Simpson公式

$$\int_{a}^{b} \int_{c}^{d}f(x,y)dxdy=\frac{hk}{9} \sum_{i=0}^{m} \sum_{j=0}^{n} w_{i,j}f(x_i,y_j)$$

其中$w_{i,j}$可通过查表获得。

截断误差为

$$E(f)=-\frac{(d-c)(b-a)}{180} \left( h^4 \frac{\partial^4f(\eta,\mu)}{\partial x^4}+k^4 \frac{\partial^4 f(\bar{\eta},\bar{\mu})}{\partial y^4} \right)$$

其中$\eta, \bar{\eta} \in [a,b],\mu,\bar{\mu} \in [c,d]$

Gauss型积分

$I(f)=\int_{a}^{b} f(x) dx$关于积分节点$\lbrace x_1,x_2, \cdots ,x_n \rbrace$的数值积分公式

$$I_{n}(f)=\sum_{i=1}^{n} \alpha_{i}f(x_i)$$

的代数精度不超过$2n-1$阶。

Legendre多项式

n次多项式

$$L_n(x)=\frac{1}{2^n n!} \frac{d^n}{dx^n}(x^2-1)^n$$

为Legendre多项式，$\lbrace L_n(x) \rbrace$为$[-1,1]$上的正交多项式系，即

$$(L_n(x),L_m(x))=\int_{-1}^{1} L_n(x)L_m(x)dx=0, m \neq n$$

$L_n(x)$具有如下性质：

• $L_n(x)$在$(-1,1)$上有n个相异的实根$x_1^{(n)},x_2^{(n)}, \cdots ,x_n^{(n)}$
• $L_n(x)$在$[-1,1]$上正交于任何一个不高于n-1次的多项式，即若$P(x)$为一个不高于n-1次的多项式，则 $$(L_n(x),P(x))=\int_{-1}^{1} L_n(x)P(x)dx=0$$

Gauss-Legendre积分

对$I(f)=\int_{-1}^{1}f(x)dx$，若选取Legendre多项式$L_n(x)$的前n个零点$x_1^{(n)},x_2^{(n)}, \cdots ,x_n^{(n)}$为数值积分节点，则其数值积分公式

$$I_n(f)=\sum_{i=1}^n \alpha_{i}^{(n)} f(x_i^{(n)})$$

具有2n-1阶代数精度。

具有n个积分节点，代数精度为2n-1的数值积分，称为Gauss积分，记为$G(f)$，$[-1,1]$上的Gauss积分公式为

$$G_n(f)=\sum_{i=1}^n \alpha_{i}^{(n)} f(x_i^{(n)})$$

其中，$x_1^{(n)},x_2^{(n)}, \cdots ,x_n^{(n)}$为正交多项式$L_n(x)$的n个零点，而

$$\alpha_{i}^{(n)}=\int_{-1}^{1}\frac{(x-x_1^{(n)}) \cdots (x-x_{i-1}^{(n)})(x-x_{i+1}^{(n)}) \cdots (x-x_n^{(n)})}{(x_i^{(n)}-x_1^{(n)}) \cdots (x_i^{(n)}-x_{i-1}^{(n)})(x_i^{(n)}-x_{i+1}^{(n)}) \cdots (x_i^{(n)}-x_n^{(n)})}dx$$

对于一般的数值积分$I(f)=\int_{a}^{b} f(x)dx$，Gauss积分公式可由线性代换获得，即

$$G_n(f)=\frac{b-a}{2} \sum_{i=1}^n \alpha_{i}^{(n)} f \left( \frac{(a+b)+(b-a)x_i^{(n)}}{2} \right)$$

$x_i^{(n)}$和$\alpha_i^{(n)}$可以通过查表获得。

Gauss型积分具有较好的性质，比如说高阶公式的稳定性质。

数值微分

在数值计算中，导数用差商作为近似值。最简单的计算方法是用函数的差商近似函数的导数，即取极限的近似值。
以下是三种差商形式的数值微分公式以及相应的截断误差：

• 向前差商
  用向前差商近似导数有 $$f'(x_0) \approx \frac{f(x_0+h)-f(x_0)}{h}$$ 用泰勒展开可得截断误差$R(x)=-\frac{h}{2}f’’(\xi)=O(h)$
• 向后差商
  用向后差商近似导数有 $$f'(x)=\frac{f(x_0)-f(x_0-h)}{h}$$ 截断误差为$R(x)=O(h)$
• 中心差商
  用中心差商近似导数有 $$f'(x)=\frac{f(x_0+h)-f(x_0-h)}{2h}$$ 截断误差为$R(x)=-\frac{h^2}{6}f’’’(\xi)=O(h^2)$

差商$\frac{f(x_0+h)-f(x_0)}{h}$表示过$(x_0,f(x_0))$和$(x_0+h,f(x_0+h))$两点直线的斜率，用近似值内接弦的斜率代替准确值切线的斜率。

设定最佳步长

在计算数值导数时，误差由截断误差与舍入误差组成。如果通过误差表达式确定步长，则可行性较差。因此，通常用事后估计的方法选取步长。

例如，记$D(h,x),D \left( \frac{h}{2},x \right)$为步长为$h,\frac{h}{2}$的差商计算公式$f’(x)$，给定误差界$\epsilon$，当$| D(h,x)-D \left( \frac{h}{2},x \right)|<\epsilon$时，步长$h$就是最合适的步长。

插值型数值微分

设$\lbrace x_i,i=0,1, \cdots ,n \rbrace$为$[a,b]$上的节点，给定$\lbrace(x_i,f(x_i)),i=0,1, \cdots ,n \rbrace$。以$(x_i,f(x_i))$为插值点构造插值多项式并近似导数。

$$f(x)=L_n(x)=\sum_{i=0}^nl_i(x)f(x_i)$$ $$f'(x)=L_n'(x)=\sum_{i=0}^nl_i'(x)f(x_i)$$

当$x=x_j$时，$f’(x_j)=L_n’(x)=\sum_{i=0}^nl_i’(x_j)f(x_i),j=0,1,\cdots,n$

误差项为

$$R(x)=\frac{d}{dx}\left(\frac{f^{(n+1)}(\xi)}{(n+1)!} \prod_{i=0}^{n}(x-x_i) \right)$$ $$R(x_j)=\prod_{i=0 \; \mathrm{and} \; i \neq j}^{n} (x_j-x_i) \frac{f^{(n+1)}(\xi)}{(n+1)!}$$