数值分析学习笔记--插值

一组离散数据点在一个外延的插值

如有疏漏，敬请指正。

插值是一种常用的函数逼近方法，上图是一个插值的例子。

Lagrange插值

Lagrange插值从线性插值出发，并逐步推广到n次多项式插值，免除了解方程组的计算。

插值多项式

对于$n+1$个不同的插值节点$\lbrace (x_{i},f(x_{i})), i=0,1,2, \cdots ,n \rbrace$，由n次插值多项式的唯一性(用待定系数法证明)，对每一个插值节点$x_{i}$作出相应的插值基函数，得到插值多项式如下

$$L_{n}(x)=\sum_{i=0}^{n} l_{i}(x)f(x_{i})$$

其中

$$l_{i}(x)=\frac{(x-x_{0})\cdots (x-x_{i-1})(x-x_{i+1})\cdots (x-x_{n})}{(x_{i}-x_{n})\cdots (x_{i}-x_{i-1})(x_{i}-x_{i+1})\cdots (x_{i}-x_{n})}$$

写得简单一点就是这样

$$l_{i}(x)=\prod_{ 0 \leq j \leq n \; and \; j \neq i } \frac{x-x_{j}}{x_{i}-x_{j}}$$

插值误差

设$L_{n}(x)$是$[a,b]$上过$\lbrace (x_{i},f(x_{i})), i=0,1,2, \cdots ,n \rbrace$的n次插值多项式，$x_{i} \in [a,b]$且互不相同，当$f \in C^{n+1}[a,b]$时，插值多项式的误差

$$R_{n}(x)=\frac{f^{(n+1)}(\zeta )}{(n+1)!}(x-x_{0})(x-x_{1}) \cdots (x-x_{n})$$

其中$\zeta \in [a,b]$

证明略去

Newton插值

Newton插值多项式是Lagrange插值多项式在不同基下的不同表达形式，Newton插值克服了Lagrange插值没有承袭性质的缺点。

Newton插值需要使用差商计算。

差商

函数$f(x)$关于点的零阶到k阶差商分别定义如下：

$$f[x_{0}]=f(x_{0})$$ $$f[x_{0},x_{1}]=\frac{f(x_{1})-f(x_{0})}{x_{1}-x_{0}}$$ $$f[x_{0},x_{1},x_{2}]=\frac{f[x_{1},x_{2}]-f[x_{0},x_{1}]}{x_{2}-x_{0}}$$ $$\cdots$$ $$f[x_{0},x_{1},\cdots ,x_{k}]=\frac{f[x_{1},x_{2},\cdots ,x_{k}]-f[x_{0},x_{1}, \cdots ,x_{k-1}]}{x_{k}-x_{0}}$$

设$f(x)$在包含$x_{0}$和$x_{1}$的区间上可微，则由中值定理得

$$f[x_{0},x_{1}]=f'(\zeta ),\zeta \in [x_{0},x_{1}]$$

这里列举差商的如下三条性质：

• k阶差商$f[x_{0},x_{1}, \cdots ,x_{k}]$是由函数值$f(x_{0}),f(x_{1}), \cdots ,f(x_{k})$线性组合而成 $$f[x_{0},x_{1}, \cdots ,x_{k}]=\sum_{i=0}^{k} \frac{1}{(x_{i}-x_{0})\cdots (x_{i}-x_{i-1})(x_{i}-x_{i+1})\cdots (x_{i}-x_{k})} f(x_{i})$$
• 若$\lbrace i_{0},i_{1}, \cdots i_{k} \rbrace$是$\lbrace 0,1,\cdots ,k \rbrace$的任一排列，则 $$f[x_{0},x_{1},\cdots ,x_{k}]=f[x_{i_{0}},x_{i_{1}}, \cdots ,x_{i_{k}}]$$
• 若$f(x)$为m次多项式，则$f[x_{0},x_{1},\cdots,x_{k-1},x]$为$m-k$次多项式

差商可以使用差商表进行计算

差商表

插值多项式与余项

对于$n+1$个不同的插值节点$\lbrace (x_{i},f(x_{i})), i=0,1,2, \cdots ,n \rbrace$，其n次Newton插值多项式为

$$N_{n}(x)=f(x_{0})+(x-x_{0})f[x_{0},x_{1}]+ \cdots +(x-x_{0})(x-x_{1}) \cdots (x-x_{n-1})f[x_{0},x_{1}, \cdots ,x_{n}]$$

余项为

$$R_{n}(x)=(x-x_{0})(x-x_{1})\cdots (x-x_{n})f[x,x_{0},x_{1},\cdots ,x_{n}]$$

Lagrange插值多项式的余项与Newton插值多项式的余项完全相等。

Hermite插值

Hermite插值可以让在节点处的插值函数与被插函数的一阶导数或更高阶导数值也相等。

插值多项式

$f(x)$关于节点$\lbrace x_{i},i=0,1, \cdots ,n \rbrace$的$n+1$个节点的$2n+1$次Hermite插值多项式为

$$H_{2n+1}(x)=\sum_{i=0}^{n} h_{i}(x)f(x_{i})+\sum_{i=0}^{n}g_{i}(x)f'(x_{i})$$

其中

$$h_{i}(x)=\left( 1-2(x-x_{i})\sum_{j \neq i} \frac{1}{x_{i}-x_{j}} \right)l_{i}^{2}(x)$$ $$g_{i}(x)=(x-x_{i})l_{i}^{2}(x)$$

其中$l_{i}(x)$是关于节点$\lbrace x_{i},i=0,1, \cdots , n \rbrace$的Lagrange基函数。

插值误差

当$f \in C^{2n+2}[a,b]$时，误差为

$$R(x)=\frac{f^{(2n+2)}(\zeta )}{(2n+2)!}(x-x_{0})^{2}(x-x_{1})^{2} \cdots (x-x_{n})^{2}, \zeta \in [a,b]$$

扩展Newton插值

这里引入推广的差商定义。

设$f(x)$充分可微，定义

$$f[x_{0},x_{0}]=f'(x)$$ $$f[x_{0}, \cdots ,x_{0}]=\frac{1}{n!}f^{(n)}(x_{0})$$

对于一部分节点相同的情况，则按如下定义

$$f[x_{0},x_{0},x_{1}]=\frac{f[x_{0},x_{1}]-f'(x_{0})}{x_{1}-x_{0}}$$

对给定的插值点的函数值和一阶导数值$(x_{i},f(x_{i}),f’(x_{i})),i=0,1,\cdots ,n$，定义序列$\lbrace z_{2i}=z_{2i+1}=x_{i},i=0,1, \cdots ,n \rbrace$，用Newton插值构造Hermite插值多项式，其中

$$z_{0}=z_{1}=x_{0},z_{2}=z_{3}=x_{1}, \cdots ,z_{2n}=z_{2n+1}=x_{n}$$ $$f[z_{2i-1},z_{2i}]=\frac{f(z_{2i})-f(z_{2i-1})}{z_{2i}-z_{2i-1}}$$ $$f[z_{2i},z_{2i+1}]=f'(x_{i}),i=0,1, \cdots ,n$$

在差商表中用$f’(x_{0}),f’(x_{1}), \cdots ,f’(x_{n})$代替$f[z_{0},z_{1}],f[z_{2},z_{3}], \cdots ,f[z_{2n},z_{2n+1}]$，其余差商公式不变，得到差商型Hermite插值公式

$$H_{2n+1}(x)=f[z_{0}]+\sum_{k=1}^{2n+1}f[z_{0},z_{1},\cdots ,z_{k}](x-z_{0})(x-z_{1}) \cdots (x-z_{k-1})$$

分段插值

Runge现象

插值多项式在插值区间内发生剧烈震荡的现象称为Runge现象，Runge现象揭示了高次插值多项式的缺陷。

下图是Runge现象的一个例子，其中红色曲线是Runge函数，蓝色曲线是5阶多项式，绿色曲线是9阶多项式。随着阶次的增加，误差逐渐变大。

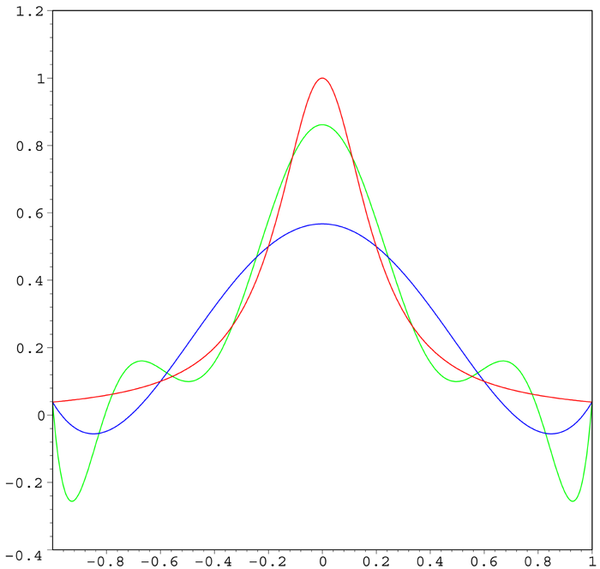
Runge现象

分段线性插值

在每个小区间$[x_{i},x_{i+1}]$上作以$\lbrace x_{i},x_{i+1} \rbrace$的线性插值$p_{i}(x)$，则

$$p_{i}(x)=\frac{x-x_{i+1}}{x_{i}-x_{i+1}}f(x_{i})+\frac{x-x_{i}}{x_{i+1}-x_{i}}f(x_{i+1})$$

然后，将线性插值函数连接即可，其误差为

$$\mid f(x)-p(x) \mid \leq \frac{M_{2}}{8}(x_{i+1}-x_{i})^{2}$$

其中

$$M_{2}=\max_{a \leq x \leq b} \mid f^{(2)}(x) \mid$$

当区间分割加密时，分段线性插值收敛于$f(x)$。

分段线性插值算法简单，其缺点是在插值节点处不光滑。

三次样条插值的M关系式

给定区间$[a,b]$上n+1个节点$a=x_{0}<x_{1}< \cdots <x_{n}=b$和这些点上的函数值$\lbrace f(x_{i})=y_{i} ,i=0,1, \cdots ,n \rbrace$，要在每个子区间$[x_{i},x_{i+1}]$上构造三次多项式

$$S(x)=S_{i}(x)=a_{i}x^3+b_{i}x^2+c_{i}x+d_{i},x \in [x_{i},x_{i+1}],i=0,1, \cdots ,n-1$$

共需要4n个条件，由插值条件$\lbrace S(x_{i})=y_i,i=0,1, \cdots ,n \rbrace$提供了n+1个条件，用每个内点的关系建立条件

$$S(x_{i}+0)=S(x_{i}-0)$$ $$S'(x_{i}+0)=S'(x_{i}-0)$$ $$S''(x_{i}+0)=S''(x_{i}-0),i=1,\cdots ,n-1$$

又得到3n-3个条件，再附加两个边界条件，即可唯一确定样条函数了，样条函数的存在性与唯一性可用待定系数法证明。

引入记号$M_{i}=S’’(x_{i})，m_{i}=S’(x_{i}),i=0,1, \cdots ,n$。用节点处的二阶导数表示样条插值函数时称为大M关系式，用一阶导数表示样条插值函数时称为小m关系式。

M关系式可以表示为如下形式

$$S(x)=\frac{(x_{i+1}-x)^3M_{i}+(x-x_{i})^{3}M_{i+1}}{6h_{i}}+\frac{(x_{i+1}-x)y_{i}+(x-x_{i})y_{i+1}}{h_{i}} \\ -\frac{h_{i}}{6}[(x_{i+1}-x)M_{i}+(x-x_{i})M_{i+1}]$$

其中$x \in [x_{i},x_{i+1}],h_{i}=x_{i+1}-x_{i}$

样条插值的M关系方程组是

$$\mu_{i}M_{i-1}+2M_{i}+ \lambda_{i}M_{i+1} =d_{i},i=1,2, \cdots ,n-1$$

其中

$$\lambda_{i} = \frac{h_{i}}{h_{i}+h_{i-i}}, \mu_{i}=1-\lambda_{1}$$ $$d_{i}=\frac{6}{h_{i}+h_{i+1}}\left( \frac{y_{i+1}-y_{i}}{h_{i}}-\frac{y_{i}-y_{i-1}}{h_{i-1}} \right)=6f(x_{i-1},x_{i},x_{i+1})$$

下面讨论边界条件

• 如果给定$M_{0},M_{1}$的值，此时方程组有n-1个未知量$\lbrace M_{i},i=1,2, \cdots ,n-1 \rbrace$。当$M_{0}=0,M_{n}=0$时，称为自然边界条件。 $$\begin{bmatrix} 2 & \lambda_{1} & & \\ \mu_{2} & 2 & \lambda_{2} & & \\ & \ddots & \ddots & \ddots & \\ & & \mu_{n-2} & 2 & \lambda_{n-2} \\ & & & \mu_{n-1} & 2 \end{bmatrix} \begin{bmatrix} M_{1} \\ M_{2} \\ \vdots \\ M_{n-2} \\ M_{n-1} \end{bmatrix} = \begin{bmatrix} d_{1}-\mu_{1}M_{0} \\ d_{2} \\ \vdots \\ d_{n-2} \\ d_{n-1}-\lambda_{n-1}M_{n} \end{bmatrix}$$
• 如果给定$S’(x_{0})=m_{0},S’(x_{n})=m_{n}$，将其分别代入$S’(x)$在$[x_{0},x_{1}],[x_{n-1},x_{n}]$中的表达式，得到 $$2M_{0}+M_{1}=\frac{6}{h_{0}}[f[x_{0},x_{1}]-m_{0}]=d_{0}$$ $$M_{n-1}+2M_{n}=\frac{6}{h_{n-1}}[m_{n}-f[x_{n-1},x_{n}]]=d_{n}$$ 得到n+1个未知量 $$\begin{bmatrix} 2 & 1 & & & & \\ \mu_{1} & 2 & \lambda_{1} & & &\\ & \mu_{2} & 2 & \lambda_{2} & & \\ & & \ddots & \ddots & \ddots & &\\ & & & \mu_{n-2} & 2 & \lambda_{n-1} \\ & & & & 1 & 2 \end{bmatrix} \begin{bmatrix} M_{0}\\ M_{1} \\ M_{2} \\ \vdots \\ M_{n-1} \\ M_{n} \end{bmatrix} = \begin{bmatrix} d_{0} \\ d_{1} \\ d_{2} \\ \vdots \\ d_{n-1} \\ d_{n} \end{bmatrix}$$
• 被插函数以$x_{n}-x_{0}$为基本周期时，即$f(x_{0})=f(x_{n})$时，即 $$S(x_{0})=S(x_{n}),S'(x_{0})=S'(x_{n}),S''(x_{0})=S''(x_{n})$$ 即$m_{0}=m_{n},M_{0}=M_{n}$，将$S’(x_{0})=S’(x_{n})$加入方程组，此时化为n个变量。

三次样条插值的m关系式

m关系式可表示为如下形式

$$S(x)=\left( 1-2\frac{x-x_{i}}{x_{i}-x_{i+1}} \right)\left( \frac{x-x_{i+1}}{x_{i}-x_{i+1}} \right)^{2}y_{i}+(x-x_{i})\left( \frac{x-x_{i+1}}{x_{i}-x_{i+1}} \right)^{2}m_{i} \\ +\left( 1-2\frac{x-x_{i+1}}{x_{i+1}-x_{i}} \right)\left( \frac{x-x_{i}}{x_{i+1}-x_{i}} \right)^{2}y_{i+1}+(x-x_{i+1})\left( \frac{x-x_{i}}{x_{i+1}-x_{i}} \right)^{2}m_{i+1}$$

样条插值的m关系方程组是

$$\lambda_{i}m_{i-1}+2m_{i}+\mu_{i}m_{i+1}=c_{i},i=1,2,\cdots ,n-1$$ $$\lambda_{i}=\frac{h_{i}}{h_{i}+h_{i-1}},\mu_{i}=1-\lambda_{i},c_{i}=3[\lambda_{i}y[x_{i-1},x_{i}]+\mu_{i}y[x_{i},x_{i+1}]]$$

再附加两个边界条件，即可解出$m_{i}$的值。